View
账号
视图状态是执行器执行过程中读写的对象,常见的视图状态模型有 UTXO 及账户两种。在 UTXO 模型中,由 UTXO 构成账本视图,每个交易在销毁旧有 UTXO 的同时创造新的 UTXO;在账户模型中,由账户构成世界状态视图,交易在处理过程中可以读写多个账户。 账户模型相对更加简单,实现通用任务更有效率。在企业级应用中往往存在身份验证与授权的需要,这些服务所依赖的数据可以自然的与账户模型关联。CITA 默认支持账户模型。用户可以自定义包括 UTXO 在内的其他状态模型。
在 CITA 中存在两种账号:外部账号和合约账号。外部账号通常情况下代表用户的身份,用户可以通过外部账号来发送交易。与公链不同,CITA 具有用户准入机制。首先用户自行生成私钥和公钥,私钥由用户妥善保存; 然后将公钥通过链外的方式提交给 CITA 系统中的 KYC 系统;通过申请之后,系统管理员将用户公钥通过操作账户管理合约,发送交易将用户加入 CITA 网络中。对于未准入的外部账户,无法向 CITA 发送交易。同时,CITA 内置了基于角色的权限管理,系统管理员(角色)可以根据实际情况灵活配置账户的权限。
为了阻止重放攻击,每笔交易必须有 nonce,这就使得账户需要跟踪 nonce 的使用情况。CITA 中用户可以根据实际业务需求,自定义 nonce 防重放机制。现阶段 CITA 兼容了 Ethereum 的自增 nonce 的防重放机制。
总体来讲,外部账户具有以下特性:
外部账号需要准入机制;
通过私钥控制,可以发送交易;
同一账户可以支持多种签名;
支持用户自定义的交易放重放规则。
合约账户与外部账户最大的区别在于,合约账户通过交易进行创建,合约内部维护一定的代码,合约的执行和调用通过外部账户发送交易来进行。当前 CITA 支持 EVM 虚拟机,用户可以通过直接发送合约代码的方式来创建合约,也可以通过合约调用的方式来创建合约。
总体来讲,合约账户具有以下特性:
合约账号通过交易创建,并支持合约创建合约;
合约通过交易调用,并支持合约间互相调用;
合约具有图灵完备性,但是交易对计算资源的配额受系统合约控制;
合约维持自身的特定储存状态;
CITA 内置系统合约模块,在创始块中生成,方便用户对系统进行管理。
存储
区块链本质上去中心化的分布式复制状态机,每个节点通过持久化的方式来保存自身的状态。CITA 使用 KV 持久化数据存储,支持 RocksDB、LevelDB。节点将 Block 结构,交易以及合约状态等持久化保存到 KV 数据库中。
为了更高效的检索和更新数据,区块链一般会在内存中维护某种数据结构的视图模型。对于传统的区块链,如 Bitcoin 采用了 Merkle Tree 来保存交易;Ethereum 采用了 Merkle Patricia Tree,一种改进的 Merkle Tree 来保存状态和交易。 CITA 采用了一种更高效的 AVL 来保存账户状态,并且采用了 Simple Merkle Tree 来保存交易列表和交易回执。下面我们将分别介绍这几种模型。
Merkle Tree
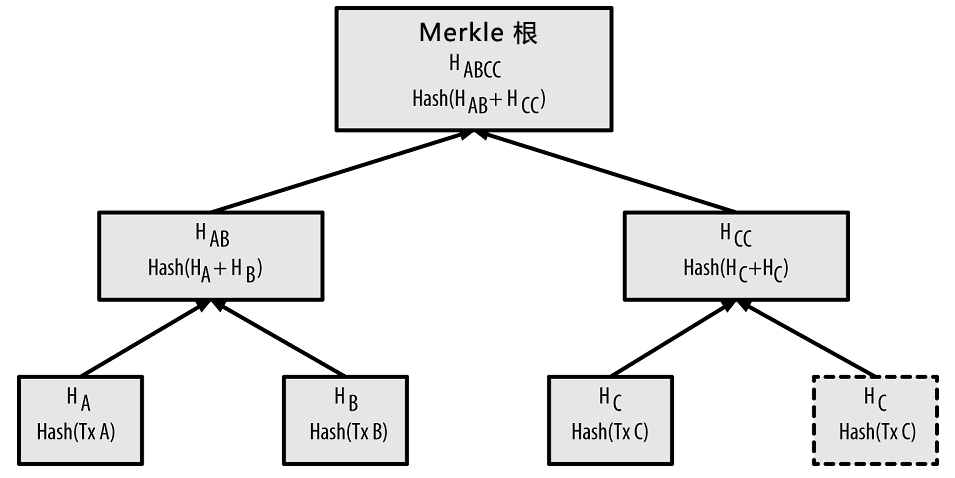
在 Bitcoin 中的每个区块都包含了产生于该区块的所有交易,且以 Merkle 树表示。Merkle 树是一种哈希二叉树,它是一种用作快速归纳和校验大规模数据完整性的数据结构。这种二叉树包含加密哈希值。
在比特币网络中,Merkle 树被用来归纳一个区块中的所有交易,同时生成整个交易集合的数字指纹,且提供了一种校验区块是否存在某交易的高效途径。生成一棵完整的 Merkle 树需要递归地对哈希节点对进行哈希,并将新生成的哈希节点插入到 Merkle 树中,直到只剩一个哈希节点,该节点就是 Merkle 树的根。
当 N 个数据元素经过加密后插入 Merkle 树时,你至多计算 2*log2(N)次就能检查出任意某数据元素是否在该树中,这使得该数据结构非常高效。同时 Merkle 树可以很好的支持轻节点。
Merkle Patricia Trie
在 Ethereum 中,使用 Trie 来构建 Merkle tree,即 Merkle Patricia Trie。它是 Ethereum 中主要的数据结构,用来存储所有账号的状态以及交易和交易回执。MPT 支持高效的检索及动态的插入、删除、修改,Ethereum 将其命名为 Merkle Patricia Tree(MPT),其示意图如下:
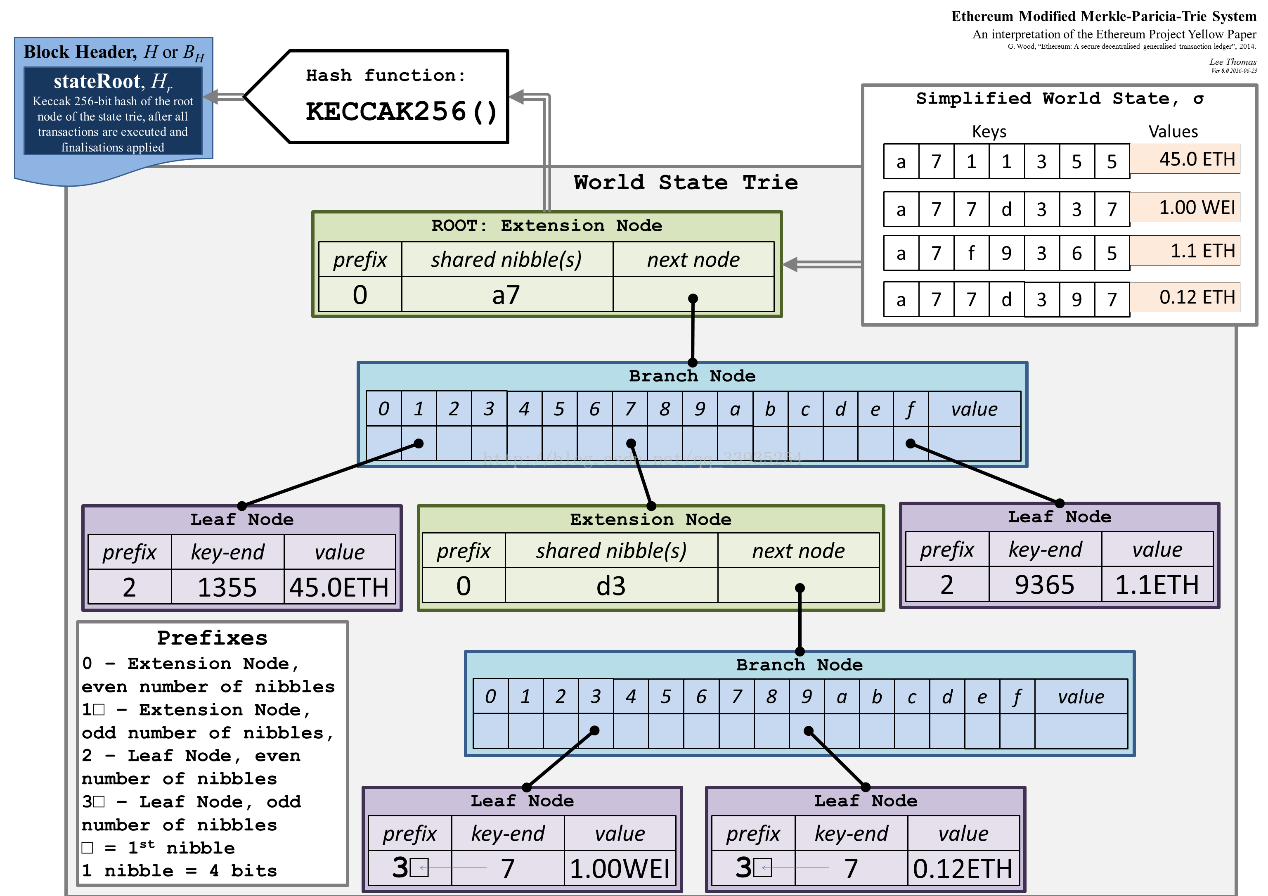
更多关于 MPT 的介绍可以参考 Ethereum Patricia-Tree。
Merkle AVL Tree
对于 Ethereum 中的 MPT,由于 Sha3 运算的开销并不低。随着账户地址的增多,以及合约存储数据量的增多,Sha3 计算的数据量也会增多。对于常见金融领域来讲,千万级数据将会导致 MPT 性能下降,Sha3 的计算将有可能成为瓶颈。 为了提高效率,我们希望在每次更新树时能够计算 Sha3 的数据量最少。对于树形结构,更新一个节点所需要重新计算的 Sha3 数据量约为 O(mlog\ :sub:m\ n),其中 m 为分支数,故当 m=2 时,Sha3 的计算量最小。 又因为 AVL Tree 的平衡性更好(尽管这意味着更多的旋转操作,幸运的是旋转操作并不增加 Sha3 计算),同时又能很好地保持 MPT 动态插入、删除、修改的特点。因此选用 AVL Tree 来构建 Merkle Tree 似乎是一个不错的选择,我们简称之为 MAT。
更多关于 AVL 的介绍可以参考 Wiki AVL_tree。
Simple Merkle Tree
在 Ethereum 中,交易和交易回执同样采用 MPT 树来进行保存。而 CITA 中,区块中的交易在共识完成后就已经确认了。所以在 Chain 处理交易时,交易的顺序和交易结果的顺序都是确定不变的。 而 MPT 树优点是便于保存历史快照可维持可变性,对于静态数据可以采用 Merkle 树,而不必采用 MPT 和 AVL 这样的数据结构。而比特币的 Merkle 树在处理奇数节点时,需要拷贝节点,额外做一次 Sha3 计算。 CITA 采用了简单的 Merkle 树来保存,对于奇数个节点情况,计算 Sha3 的次数会减少。
*
/ \
/ \
/ \
/ \
* *
/ \ / \
/ \ / \
/ \ / \
* * * h6
/ \ / \ / \
h0 h1 h2 h3 h4 h5